5月iOS設備性能榜：M1 M2依舊是榜單前五
和上個月一樣，沒有新品發布的iOS設備性能榜的上榜設備并沒有什么更替，僅僅只有跑分變化而產生的排名變動，剛剛開始的蘋果WWDC2023，推出的產品也依舊是新款Mac Pro、新款Mac Stu
平穩性是時間序列分析與預測的核心概念。在平穩條件下，時間序列的統計特性（如均值）在時間維度上保持不變，僅存在隨機波動。
但是實際數據集中很少觀察到完全的平穩性。時間序列通常會經歷結構性斷裂或變化。這些變化會引入非平穩性，從而改變時間序列的整體分布，這些標志著變化開始的時間點被稱為變化點。
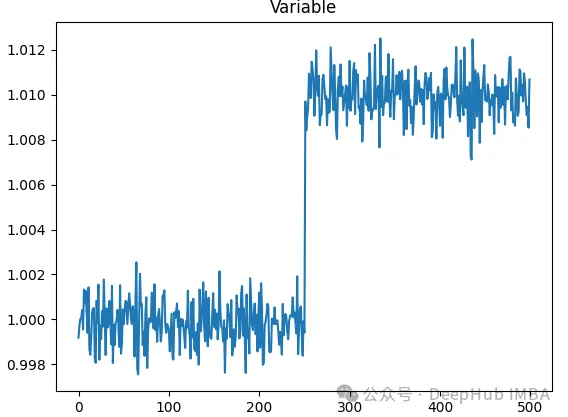
在時間序列分析和預測中，準確檢測結構變化至關重要。新出現的分布模式往往會導致歷史數據失去代表性，進而影響基于這些數據訓練的模型的有效性。因此需要采用最新數據更新模型或采取其他適當策略。對于歷史數據中的變化點，可以通過特征工程方法（如干預分析）進行處理。
但需要注意的是，結構變化與異常值是兩個不同的概念。異常值是指與時間序列的基本結構或分布所定義的正常行為顯著偏離的觀測值。而變化點則是指時間序列的整體結構發生轉變，導致分布特性的改變。
接下來，我們首先詳細探討不同類型的結構變化。
結構變化可以分為多種類型。深入理解這些變化的性質對于選擇適當的處理策略至關重要。
水平變化主要體現在序列的均值或方差上。均值的變化表現為平均水平的移動，可以是永久性的，也可以是暫時性的。
永久性水平移動是指序列的平均值永久性地轉移到一個新的水平。例如當一家零售企業開設新店時，銷售時間序列可能會轉移到一個更高的水平，反映出擴大的客戶基礎。
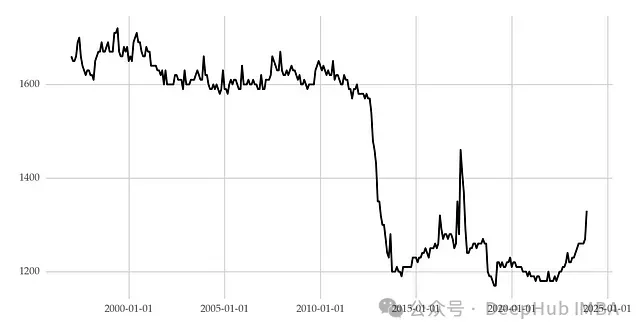
暫時性水平移動是指平均值在一段時間后恢復到原有水平。例如制造工廠的一臺機器因維修而臨時停機，生產時間序列在維修期間會出現暫時性的低值。一旦機器恢復運行，生產水平預計會回到正常狀態。
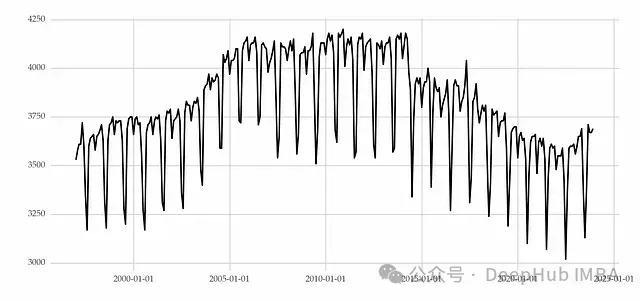
方差的變化會導致時間序列離散程度的增加或減少，具有非恒定方差的時間序列通常被稱為異方差序列。方差的變化同樣可以是永久性的或暫時性的。
方差的周期性變化是波動聚類現象的典型特征。波動聚類指的是時間序列呈現出低方差期和高方差期交替出現的模式。換言之，大（?。┓茸兓鶗B續出現。
以下是表示每小時風速變化的時間序列示例，展示了波動聚類現象：
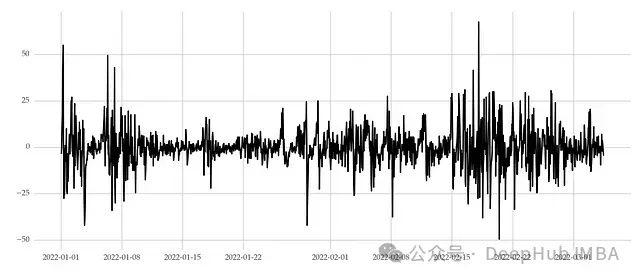
具有波動聚類特征的時間序列示例。
波動聚類在氣象學（如風速分析）和金融學（如資產價格研究）等領域中較為常見。
變化點檢測算法旨在精確識別時間序列分布發生顯著變化的時間點。本節將詳細探討多種變化點檢測方法的實際應用。
我們從 datasetsforecast 庫中加載一個示例時間序列數據：
from datasetsforecast.m4 import M4 dataset, *_ = M4.load('./data', 'Monthly') series = dataset.query(f'unique_id=="M1430"').reset_index(drop=True) series['time'] = pd.date_range(end='2023-12-01', periods=series.shape[0], freq='M')此數據集是非常有名的銷量預測比賽M4
kats是Meta開發的一個功能強大的時間序列分析庫。它提供了多種變化檢測方法，包括CUSUM（累積和）和貝葉斯在線變化點檢測等。
kats要求使用特定的數據結構，可以按以下方式進行設置：
from kats.consts import TimeSeriesData ts = TimeSeriesData(df=series[['time', 'y']])CUSUM（累積和）是一種廣泛應用于檢測時間序列均值變化的方法。其原理是計算相對于預期值的偏差累積和。如果序列的均值保持穩定，累積和將呈現圍繞零的隨機波動。累積和的持續正向（或負向）變化則表明均值發生了上升（或下降）移動。
以下代碼展示了如何使用kats中的CUSUM方法：
from kats.tests.detectors.test_cusum_detection import CUSUMDetector model = CUSUMDetector(ts) change_points = model.detector(direction=['decrease', 'increase']) model.plot(change_points)detector方法的 direction 參數用于指定需要監測的變化方向。在本例中我們同時監測序列的上升和下降變化。
CUSUM方法實現了對變化點的準確檢測：
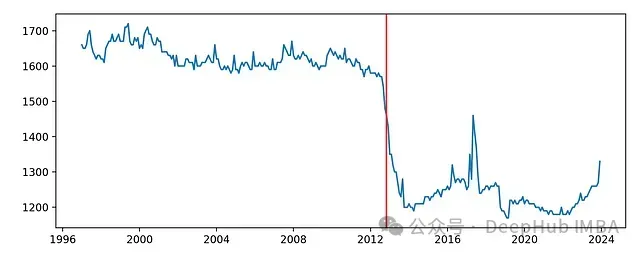
另一種與CUSUM相似的方法是在移動平均的基礎上計算z分數。kats中的 RobustStatDetector 就采用了這種方法：
from kats.tests.detectors.test_robust_stat_detection import RobustStatDetector model = RobustStatDetector(ts) change_points = model.detector(p_value_cutoff=0.001, comparison_window=12) model.plot(change_points)在這個方法中，我們將p值閾值設置為0.001，窗口大小設置為12（對應于一年的數據，因為該序列是按月收集的）。
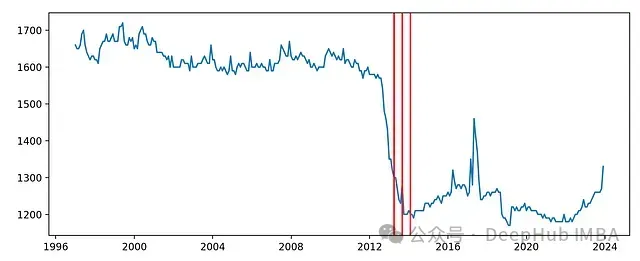
使用kats中的RobustStatDetector檢測變化點。RobustStatDetector在這個例子中檢測到了幾個相互靠近的變化點。
ruptures庫同樣提供了多種變化點檢測算法的實現，包括PELT（修剪精確線性時間）、基于核的算法和動態規劃算法等。
以下是使用PELT算法檢測均值變化的示例：
import ruptures as rpt # 將時間序列轉換為numpy數組 signal = series['y'].values # 擬合PELT模型 model = rpt.Pelt(model="rbf").fit(signal) # 獲取變化點 result = model.predict(pen=10)PELT算法的核心思想是將時間序列分割成具有不同統計特性（如均值）的多個片段。它通過最小化一個用戶定義的成本函數來實現這一目標，該函數的具體形式取決于需要檢測的變化類型。在這個例子中我們使用了基于徑向基函數的模型（model="rbf"）。
以下是PELT模型的檢測結果：
在識別出變化點后，下一步就是采取適當的處理措施。以下是幾種常用的處理方法：
對時間序列進行差分是處理均值變化的一種有效方法。這種技術通過計算連續觀測值之間的差值來穩定序列的平均水平。
以下是示例序列的一階差分結果：
差分法能夠有效消除許多類型的非平穩性，使得后續的分析和建模工作更加可靠。
另一種處理變化點的方法是引入虛擬變量。這種方法在變化點之前賦值為0，之后賦值為1，從而在模型中顯式地表示結構變化。
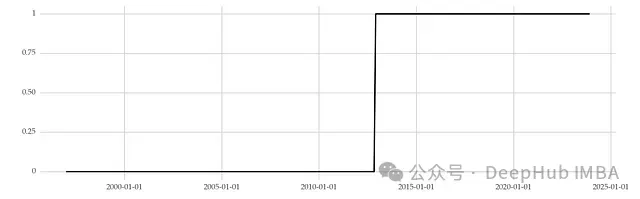
虛擬變量法允許模型捕捉變化前后的不同行為，提高了模型的靈活性和準確性。
對于暫時性變化，區制轉換模型（regime-switching）是一種較為復雜但有效的建模方法。這類模型能夠根據當前的狀態或區制采用不同的參數設置。
閾值自回歸（TAR）模型是區制轉換模型的一個典型例子。TAR模型對不同范圍的時間序列值采用不同的參數，從而能夠捕捉復雜的非線性動態。
通過本文的分析，我們可以得出以下幾點重要結論：
通過深入理解時間序列的結構變化，并靈活運用各種檢測和處理方法，分析人員可以顯著提高時間序列模型的準確性和可靠性，為決策提供更有力的支持。
本文鏈接：http://www.tebozhan.com/showinfo-26-112713-0.html時間序列結構變化分析：Python實現時間序列變化點檢測
聲明：本網頁內容旨在傳播知識，若有侵權等問題請及時與本網聯系，我們將在第一時間刪除處理。郵件：2376512515@qq.com
上一篇： 面試官：如何實現線程池任務編排？
Copyright ? 2016-2023 天津谷騏科技有限公司 版權所有 sitemap.xml
違法及侵權請聯系：2376512515@qq.com 津ICP備18001702號
津公網安備 12010102000574號